RCC Spotlight: Dr. Tom Needham

Dr. Tom Needham earned his bachelor's degree at the University of Wisconsin- Milwaukee (UWM), double majoring in applied mathematics and physics. He then continued his education at UWM and earned his master's degree in mathematics. After the completion of his master’s, Dr. Needham earned his doctorate in mathematics from the University of Georgia. He completed his postdoctoral work at Ohio State University and then began working at FSU as an assistant professor in the mathematics department. His research specializes in geometry and topology with a focus on applications to problems in data science.
Dr. Needham is interested in understanding the structure of data by using tools through a more theoretical approach. His research involves three main areas: symplectic geometry, optimal transport, and algebraic topology. Symplectic geometry is a field which was invented to give a precise mathematical framework for classical physics. In Dr. Needham’s work, symplectic geometry focuses on how measurement systems, known as frames, can be constructed and understood in a way that is both efficient and robust to noise. These frames, which involve collecting more data than needed, allow for greater resilience and more accurate reconstruction of signals. By using symplectic geometry tools, Dr. Needham investigates the geometric properties of the space of all frames and addresses questions. These questions include whether it’s possible to interpolate between two different measurement systems.
Dr. Needham’s second area of focus is optimal transport, a classical mathematics framework depicting the allocation of resources. Today, it plays a central role in data science. He uses optimal transport to model how data can be transferred from one space to another. Each model is unique as it requires him to figure out the formula for a particular pair of graphs.
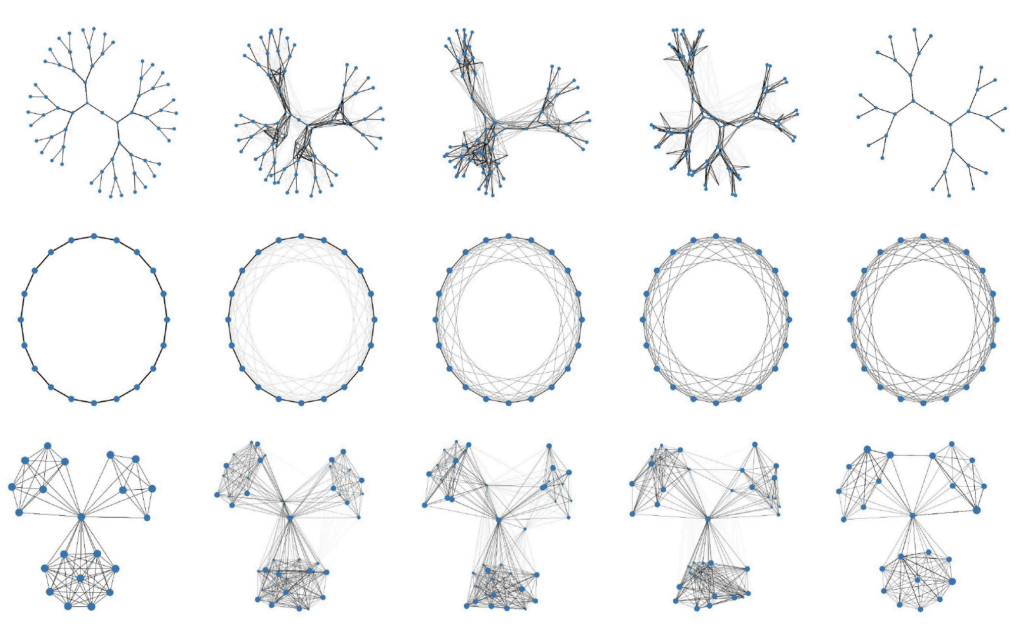
Figure 1 shows various interpolations between graphs using geometric methods developed by Needham. These visualizations can be used to discover and highlight structural similarities and differences between graphs.
Dr. Needham’s third area of research is algebraic topology; a field closely related to geometry that focuses on understanding the properties of shapes and spaces. His work takes abstract topological ideas and makes them computationally based. By translating topological features of a dataset into computation1ally friendly algebraic invariants, he transforms complex shapes into something that can be used in machine learning models. This approach is useful for analyzing highly non-linear data structures.

Figure 2 illustrates a method for matching topological features between point clouds. The algorithm combines ideas from optimal transport and topological data analysis.
As expected, projects of this size are computationally intensive, and an average computer would be very inefficient at the levels of computation needed. This is where the Research Computing Center (RCC) comes in. The RCC High Performance Compute (HPC) cluster makes Dr. Needham’s research possible by providing enough compute power to conduct optimal transport and execute topology techniques. Using the HPC, he can achieve quick turnaround and feedback to ensure the data is accurate. This is crucial in a field where things are constantly changing and evolving.
Dr. Needham is interested in how the world has become affected by machine learning and artificial intelligence. He believes that novel tools from many fields of mathematics and statistics will be necessary for understanding model training processes, with a view toward rendering models more interpretable and trustworthy.
*Figures courtesy of Dr. Tom Needham

